5.2. Instalaciones de bombeo y ventilación

5.2.1. Introducción

En este capítulo se generaliza el análisis de flujo en conductos realizado anteriormente para abordar el cálculo de instalaciones de fluidos. En particular, este capítulo se centrará en el estudio de instalaciones de bombeo y ventilación (con flujo presurizado), considerando flujo incompresible.

El objetivo de las instalaciones de bombeo es el transporte de un fluido en estado líquido. Las instalaciones de ventilación tienen el mismo objetivo, pero estando el fluido en estado gaseoso. Para vencer las pérdidas de energía por disipación viscosa, así como los gradientes de presión adversos y las variaciones de altura, habitualmente es necesario proporcionar energía al fluido mediante máquinas de fluidos generadoras de energía. En instalaciones de bombeo, las máquinas estas máquinas son bombas hidráulicas, mientras que en instalaciones de ventilación son ventiladores.

Una instalación de bombeo o ventilación se compone de los siguientes elementos:

• Máquinas de fluidos (bomba o ventilador)

• Conductos o tuberías, también llamados líneas o tramos

• Elementos singulares (codos, cambios de sección, etc.)

• Elementos de regulación (válvulas)

• Depósitos (abiertos a la atmósfera o presurizados)

• Entradas y salidas

Un ejemplo de instalación de bombeo en el que se detalla la representación esquemática de los elementos anteriores se muestra a continuación.

Fig. 5.1 Ejemplo de una instalación de bombeo.

Las máquinas de fluidos se pueden clasificar atendiendo a distintos criterios. Según el sentido de transmisión de energía, podemos hablar de máquinas generadoras si transmiten energía al fluido (bombas, ventiladores y compresores), receptoras si extraen energía del fluido (turbinas), reversibles si pueden operar como generadoras o receptoras, y finalmente transmisoras si transmiten energía entre dos sistemas mecánicos (transmisión hidromecánica). En este capítulo nos centraremos en máquinas generadoras.

Por otro lado, si atendemos al principio de funcionamiento de la máquina, se pueden clasificar en dos categorías generales: las turbomáquinas y las máquinas de desplazamiento positivo, cuya principal diferencia es que las primeras son de flujo continuo y las segundas no. A su vez, las turbomáquinas se dividen en turbomáquinas hidráulicas (bombas) y turbomáquinas térmicas (soplantes y compresores). En este capítulo consideraremos líquidos o gases bajo la hipótesis de flujo incompresible, por lo que nos centraremos en turbomáquinas hidráulicas: bombas y ventiladores.

En una turbomáquina hidráulica, la transferencia de energía de la máquina al fluido se realiza en un elemento giratorio compuesto de álabes llamado rodete. Dependiendo de cómo se mueve el fluido en relación con el rodete, podemos distinguir entre máquinas axiales, radiales y mixtas. Un ejemplo de una máquina radial es la bomba centrífuga de la figura inferior. En este tipo de bomba, el fluido entra por el centro del rodete a través del distribuidor y es impulsado por éste en dirección radial hasta la voluta (carcasa exterior de la bomba), que conduce el fluido hasta la salida.

Fig. 5.2 Vista exterior (izquierda) e interior (derecha) de una bomba hidráulica centrífuga.

El principio de funcionamiento e una bomba hidraúlica es sencillo: el rodete dispone de álabes que comunican energía cinética al fluido. La transferencia de energía la representamos matemáticamente como una potencia asociada a los esfuerzos en la superficie de contacto con los álabes, \(S_a\), que se mueven con velocidad \(\vec{\mathbf{v}}\):

\[\dot{W}_{a\rightarrow f} =\int_{S_{a}} \left(-p \hat{\mathbf{n}} + \tilde{\boldsymbol {\tau}}_v\cdot \hat{\mathbf{n}}\right)\cdot \vec{\mathbf{v}}dS\]

5.2.2. Balance energético en la instalación

Para obtener las ecuaciones de balance energético en instalaciones de fluidos aplicaremos las leyes fundamentales de conservación en forma integral estudiadas en el tema 2. Para realizar este análisis, consideraremos una instalación formada por un conducto de aspiración, la máquina de impulsión y un conducto de impulsión. Para simplificar, consideraremos una bomba como máquina de impulsión. El resultado para un ventilador sería el mismo. El volumen de control (VC) utilizado se muestra en la figura inferior, éste excluye los álabes (rodete). La superficie de control (SC) se compone de la superficie de entrada, \(S_1\), la superficie de salida, \(S_2\), la superficie de las paredes, \(S_{paredes}\), y la superficie de los álabes, \(S_a\), es decir

(5.1)\[\begin{equation} SC=S_1 \cup S_2 \cup S_{paredes} \cup S_a \end{equation}\]

Fig. 5.3 Dominio de estudio real (izquierda) y su representación esquemática (derecha) en la que se representa el volumen de control utilizado (línea de puntos) para aplicar las ecuaciones integrales. El VC excluye el rodete (en rojo).

Mediante el Tercer Teorema del Transporte de Reynolds escribimos la ecuación de conservación de la masa para este VC de la siguiente manera:

(5.2)\[\begin{equation} \underbrace{\frac{d}{dt}\int_{VC} \rho dV}_{I} + \underbrace{\int_{SC} \rho(\vec{\mathbf{v}}- \vec{\mathbf{v}}_c )\cdot \hat{\mathbf{n}}dS}_{II}=0 \end{equation}\]

donde:

• I: Es la variación temporal de la masa en el VC, que al ser un VC fijo y considerar flujo estacionario tenemos:

  \[\frac{d}{dt}\int_{VC} \rho dV=0\]

• II: Son los flujos de entrada y salida de masa, que se pueden escribir como:

  \[\int_{SC} \rho(\vec{\mathbf{v}}- \vec{\mathbf{v}}_c )\cdot \hat{\mathbf{n}}dS = (\rho Q)_2-(\rho Q)_1\]

  con \(\rho\) la densidad del fluido, que se asume constante (flujo incompresible), y \(Q\) el caudal volumétrico.

Agrupando los términos anteriores (\(I+II=0\)) se obtiene la ecuación de conservación de la masa para este VC particular

(5.3)\[\begin{equation}\label{eq:eqmasa2} ( \rho Q)_1=(\rho Q)_2 \end{equation}\]

y como \(\rho\) es constante podemos afirmar que \(Q\) es constante.

La ecuación de conservación de la energía mecánica aplicada al volumen de control es:

(5.4)\[\begin{multline}\label{eq:emec} \underbrace{\frac{d}{dt}\int_{VC} \rho \left(\frac{v^2}{2}+gz \right)dV}_{I} + \underbrace{\int_{SC} \rho \left( \frac{v^2}{2}+gz \right)(\vec{\mathbf{v}}- \vec{\mathbf{v}}_c )\cdot \hat{\mathbf{n}}dS}_{II} \\ = \underbrace{\int_{SC} \left(\tilde{\boldsymbol {\tau}} \cdot \hat{\mathbf{n}}\right)\cdot \vec{\mathbf{v}}dS}_{III}+\underbrace{\int_{VC} p\nabla\cdot\vec{\mathbf{v}} dV}_{IV} - \underbrace{\int_{VC} \Phi_v dV}_{V} \end{multline}\]

donde:

• I: Es la variación temporal de energía mecánica en el VC, que al ser un VC fijo y considerar flujo estacionario tenemos:

  \[\frac{d}{dt}\int_{VC} \rho \left( \frac{v^2}{2}+gz \right)dV=0\]

• II: Son los flujos de entrada y salida de energía mecánica:

  \[\int_{SC} \rho \left( \frac{v^2}{2}+gz \right)(\vec{\mathbf{v}}- \vec{\mathbf{v}}_c )\cdot \hat{\mathbf{n}}dS = \rho Q \left[ \left( \frac{v^2}{2}+gz \right)_2 - \left( \frac{v^2}{2}+gz \right)_1 \right]\]

• III: Es la potencia transmitida al fluido a través de las superficies de control:

  \[\int_{SC} \left(\tilde{\boldsymbol {\tau}} \cdot \hat{\mathbf{n}}\right)\cdot \vec{\mathbf{v}}dS = Qp_1-Qp_2 + \dot{W}_{a\rightarrow f} \]

• IV: Es la potencia de las fuerzas de presión en procesos reversibles de expansión y compresión, que para un flujo incompresible es 0:

  \[\int_{VC} p\cancelto{0}{\nabla\cdot\vec{\mathbf{v}}} dV = 0\]

• V: Es la potencia de disipación viscosa:

  \[\int_{VC} \Phi_v dV \geq 0\]

  donde \( \Phi_v=\tilde{\boldsymbol {\tau}}_v:\nabla\vec{\mathbf{v}}\) es la función de disipación de Rayleigh.

Agrupando los términos anteriores (\(I+II=III+IV+V\)) obtenemos:

(5.5)\[\begin{equation}\label{eq:emec2} \boxed{ \textcolor[RGB]{0, 152, 46}{ \rho Q \left[ \left( \frac{v^2}{2}+\frac{p}{\rho}+gz \right)_2 - \left( \frac{v^2}{2}+\frac{p}{\rho}+gz \right)_1 \right] } = \textcolor[RGB]{0, 0, 255}{ \dot{W}_{a\rightarrow f} } - \textcolor[RGB]{255, 100, 0}{\int_{VC} \Phi_v dV} } \end{equation}\]

que indica que la ganancia de energía mecánica más energía de presión del flujo es igual a la diferencia entre el trabajo realizado por la máquina y las pérdidas por disipación. El término \(\dot{W}_{a\rightarrow f}\) es la potencia transferida de los álabes al fluido, que contabiliza la entrada neta de energía al flujo y se expresa como

(5.6)\[\begin{equation} \dot{W}_{a\rightarrow f}=\int_{S_a} \left(\tilde{\boldsymbol {\tau}} \cdot \hat{\mathbf{n}}\right)\cdot \vec{\mathbf{v}}dS \end{equation}\]

y está asociada a la fuerza que ejercen los álabes sobre el fluido

(5.7)\[\begin{equation} \vec{\bf{F}}_{a\rightarrow f}=\int_{S_a} \tilde{\boldsymbol {\tau}} \cdot \hat{\mathbf{n}}dS \end{equation}\]

A continuación se resumen los términos presentes en las ecuaciones de conservación de la energía total, mecánica e interna, con el fin de mostrar esquemáticamente los balances de energía para cada una de ellas. En la columna Energía específica se detalla la suma de las distintas formas de energía a tener en cuenta en los flujos de entrada y salida. Por otro lado, en las columnas Fuentes de energía se detallan las distintas fuentes (\(>0\)) o sumideros (\(<0\)) de energía.

La observación más relevante que se puede realizar en esta tabla es que, como se vio en el Tema 2, la disipación viscosa es una fuente de energía interna y un sumidero de energía mecánica. La dirección de dicho proceso no se puede invertir, ya que sino no se satisfaría el Segundo Principio de la Termodinámica. En la ecuación de la energía total no participa la disipación viscosa, ya que es un mecanismo de transferencia de energía entre energía mecánica e interna.

Fig. 5.4 Flujos de energía total, mecánica e interna, así como sus respectivas fuentes y sumideros.

Fig. 5.5 Representación gráfica de los balances de energía mecánica e interna en el VC.

La ecuación de conservación de la energía interna la escribimos como

(5.8)\[\begin{equation}\label{eq:eint} \boxed{ \textcolor[RGB]{0, 152, 46}{ \rho Q \left( e_2 - e_1 \right) } = \textcolor[RGB]{255, 100, 0}{\int_{VC} \Phi_v dV} - \textcolor[RGB]{255, 0, 0}{\dot{\mathcal{Q}}} } \end{equation}\]

y podemos utilizarla para estimar el calentamiento que sufre el fluido en la instalación. Sustituyendo \(e=cT\) donde \(c\) es el calor específico del fluido, obtenemos

(5.9)\[\begin{equation} T_2 - T_1 = \frac{1}{\rho c Q}\left( \textcolor[RGB]{255, 100, 0}{\int_{VC} \Phi_v dV} + \textcolor[RGB]{255, 0, 0}{\dot{\mathcal{Q}}} \right) \end{equation}\]

observando que el calentamiento es debido a la disipación viscosa (siempre positiva) y a los flujos de calor entre el fluido y el exterior (que serán cero, si está aislado, o negativos, si cede calor al exterior).

Show code cell content Hide code cell content

from sympy import *             # Librería para trabajo simbólico
import numpy as np              # Librería para cálculo numérico
import math                     # Librería para utilizar símbolos matemáticos como el número pi, que se escribe como math.pi
import matplotlib.pyplot as plt # Librería para poder dibujar gráficas
from myst_nb import glue

g=9.81    #aceleración de la gravedad (m/s^2)
f=0.02    #factor de fricción de Darcy
L=5+500   #longitud total conductos (m)
D=0.1     #diámetro conductos (m)
z1=0      #cota depósito 1 (m)
z2=36     #cota depósito 2 (m)
rho=1000  #densidad agua (kg/m^3)
S=math.pi*D**2/4 

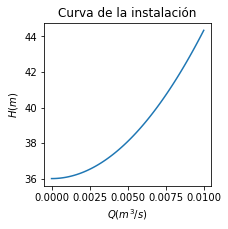
def h_inst(Q):  #curva de la instalación          
    return  z2-z1+f*L/(D*2*g)*(Q/S)**2 

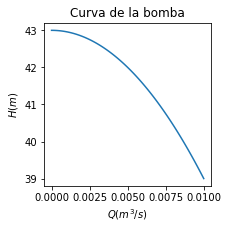
def h_bomba(Q):  #curva de la bomba (dato)        
    return  43-40000*Q**2

Lt=0.01                       #longitud del eje X (rango de caudales en m^3/s)
N = 100                       #numero de puntos a representar
xp = np.linspace(0, Lt, N)    #puntos en x
yp1 = h_inst(xp)              #puntos en y: curva instalacion
yp2 = h_bomba(xp)             #puntos en y: curva bomba

fig, ax  = plt.subplots(figsize=(3,3))     #genera el objeto "fig"
ax.plot(xp,yp1,label='Curva resistente de la instalación')                
ax.set_title('Curva de la instalación')
ax.set_xlabel("$Q(m^3/s)$") 
ax.set_ylabel("$H(m)$") 
glue("curva1", fig, display=False)

fig2, ax  = plt.subplots(figsize=(3,3))     #genera el objeto "fig"
ax.plot(xp,yp2,label='Curva de la bomba')                
ax.set_title('Curva de la bomba')
ax.set_xlabel("$Q(m^3/s)$") 
ax.set_ylabel("$H(m)$") 
glue("curva2", fig2, display=False)

Curvas

A la curva \(H_I(Q)\) se le llama curva resistente de la instalación y es una representación gráfica de la altura energética de la instalación, \(H_I\), frente al caudal:

A la curva \(H_B(Q)\) se le llama curva característica de la bomba y es una representación gráfica de la altura energética de la bomba, \(H_B\), frente al caudal:

Más adelante veremos que existen otras curvas características de la bomba.

5.2.3. Punto de operación

Por simplicidad, vamos a considerar el ejemplo de la figura inferior en la que tenemos dos depósitos conectados por un conducto en el que hay una bomba.

Fig. 5.6 Instalación sencilla.

Dividiendo la ecuación de conservación de la energía mecánica por \(\rho g Q\) (donde \(Q\) es el caudal volumétrico) obtenemos la ecuación de la energía mecánica en términos de alturas energéticas:

(5.10)\[\begin{equation}\label{eq:emec_alturas} \boxed{ \left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_2 - \left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_1 = H_B - H_f } \end{equation}\]

donde la energía aportada por la bomba en términos de altura energética, o altura de la bomba, es

(5.11)\[\begin{equation}\label{eq:hb_def} H_B=\frac{\dot{W}_{a\rightarrow f}}{\rho g Q} \end{equation}\]

y la energía de pérdidas viscosas, o altura de pérdidas, es

(5.12)\[\begin{equation} H_f=\frac{{\int_{VC} \Phi_v dV}}{\rho g Q} \end{equation}\]

Por otro lado, el término \(\left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_2\) es la altura energética a la salida y el término \(\left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_1\) es la altura energética a la entrada.

Podemos reordenar la ecuación de la energía mecánica en la instalación de la siguiente manera

(5.13)\[ \underbrace{\left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_2 - \left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_1 + H_f(Q) }_{H_I(Q)} = H_B(Q)\]

dejando a la izquierda de la igualdad todo lo que depende de la instalación y a la derecha todo lo que depende de la bomba, siendo:

• \(H_I(Q)\): Función altura de la instalación, una relación entre la altura energética y el caudal de la instalación. Es la altura energética requerida para mover un caudal \(Q\). Depende de la instalación (entrada, salida, conductos, elementos singulares…). La calcularemos de la siguiente manera:

(5.14)\[\begin{equation}\label{eq:curva_inst} H_I(Q)\equiv\left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_2 - \left( \frac{v^2}{2g}+\frac{p}{\rho g}+z \right)_1 + H_f \end{equation}\]

(5.15)\[\begin{equation}\label{eq:perdidas} H_f= H_{L} + \sum H_{S,j} =\left( \frac{fL}{D} + \sum k_{m,j}\right)\frac{Q^2}{2gS^2} \end{equation}\]

• \(H_B(Q)\): Función altura de la bomba, una relación entre la altura energética y el caudal de la bomba. Es la altura energética aportada para mover un caudal \(Q\). Depende de la bomba, proporcionada por el fabricante.

La ecuación (5.13) indica lo siguiente: La energía aportada por la bomba (altura de la bomba) debe ser igual a la energía requerida para hacer circular el fluido en la instalación (diferencia de alturas entre salida y entrada más la altura de pérdidas por disipación).

A los términos \(H_I(Q)\) y \(H_B(Q)\) también se les llama curva resistente de la instalación y curva característica de la bomba, respectivamente, y se muestran en el margen derecho.

Punto de operación de una instalación

Matemáticamente, el punto de operación es la solución de la ecuación (5.13)

(5.16)\[\begin{equation} H_I(Q)=H_B(Q) \end{equation}\]

donde \(H_I(Q)\) es la curva de la instalación y \(H_B(Q)\) es la curva de la máquina, proporcionada por el fabricante.

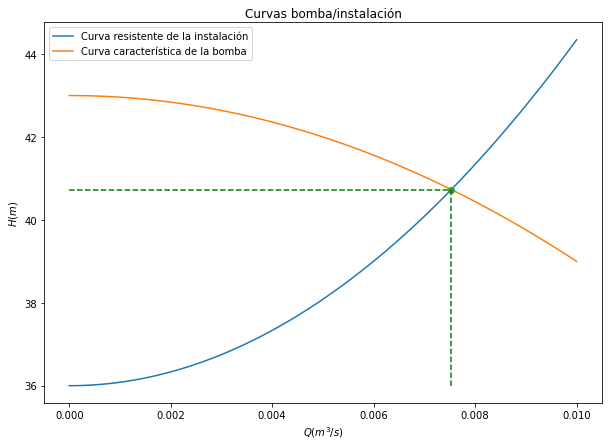
Desde un punto de vista gráfico, a la intersección entre la curva resistente de la instalación, \(H_I(Q)\), y la curva característica de la máquina, \(H_B(Q)\), se le denomina punto de operación. En la figura inferior se representan de manera cualitativa las curvas de la máquina y de la instalación, así como el punto de operación denotado por \((Q^{\star},H^{\star})\).

Fig. 5.7 Punto de operación

5.2.4. Curvas características de la bomba

Las curvas características de las bombas hidráulicas son relaciones funcionales que permiten expresar las variables de interés (altura energética, potencia y rendimiento) en función del caudal. Estas curvas son herramientas fundamentales para entender el comportamiento y el rendimiento de una bomba en diferentes condiciones de operación. Las curvas características de una bomba hidráulica se obtienen experimentalmente y son específicas para cada modelo de bomba. Cada bomba tiene su propia curva característica debido a su diseño, tamaño y construcción.

Antes de explicar las distintas curvas características, es necesario definir el concepto de rendimiento de una bomba hidráulica.

Rendimiento de una bomba

El rendimiento de una bomba hidráulica se define como la relación entre la potencia transmitida al fluido y la potencia en el eje

(5.17)\[\begin{equation}\label{eq:bcar2} \eta= \frac{\dot{W}_{a\rightarrow f}}{\dot{W}_{eje}}=\frac{\rho g Q H_B(Q)}{T\Omega} \end{equation}\]

con \(T\) el par motor y \(\Omega\) la velocidad angular de giro. Este rendimiento también depende del caudal y se ve afectado por las pérdidas hidráulicas y mecánicas, alcanzando un máximo para cierto valor de caudal, denominado caudal de diseño de la máquina.

Mediante el análisis dimensional, es posible expresar los números adimensionales de las variables de interés en función solamente del caudal adimensionalizado, \(\frac{Q}{\Omega D^3}\), asumiendo semejanza parcial (para altos números de Reynolds la influencia de éste es pequeña):

\[ \frac{gH_B}{\Omega^2D^2}=\Pi_1\left(\frac{Q}{\Omega D^3} \right), \quad \eta=\Pi_2\left(\frac{Q}{\Omega D^3} \right), \quad \frac{\dot{W} }{\rho\Omega^3D^5}=\Pi_3\left(\frac{Q}{\Omega D^3} \right) \]

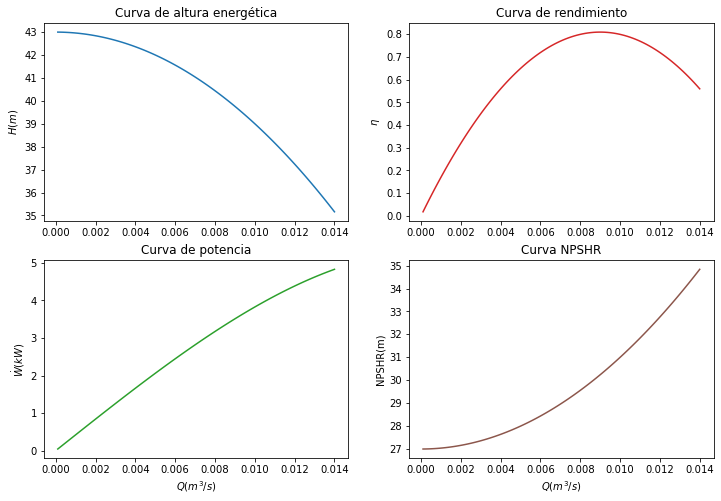
En la Figura inferior se muestran la forma habitual de las curvas características en forma adimensional para la altura energética, la potencia y el rendimiento.

Fig. 5.8 Curvas características en forma adimensional.

Desde un punto de vista práctico, lo más habitual es trabajar con la forma dimensional de las curvas características. Estas curvas en forma dimensional se obtienen fijando un valor de \(\Omega\) y de \(D\), lo que permite representar las variables de interés frente al caudal. Se trabajará con las siguientes:

• Curva de altura-caudal, \(H_{B}(Q)\): representa la altura energética aportada en función del caudal \(Q\).

• Curva de rendimiento, \(\eta(Q)\): representa el rendimiento de la bomba en función del caudal \(Q\).

• Curva de potencia, \(\dot{W}(Q)\): representa la potencia aportada por la bomba en función del caudal \(Q\).

• Curva NPSHR (Net Positive Suction Head Required): representa altura energética neta positiva de aspiración requerida, en función del caudal \(Q\). Es decir, la energía mínima necesaria que el fluido debe tener, en la toma aspiración de la bomba, para garantizar un funcionamiento adecuado. El objetivo es garantizar que la presión de aspiración sea superior a la presión de vapor del líquido en la entrada del rodete, evitando así la cavitación.

A continuación se muestra la forma típica de estas cuatro curvas características en su forma dimensional.

Show code cell content Hide code cell content

g=9.81    #aceleración de la gravedad (m/s^2)
f=0.02    #factor de fricción de Darcy
L=5+500   #longitud total conductos (m)
D=0.1     #diámetro conductos (m)
z1=0      #cota depósito 1 (m)
z2=36     #cota depósito 2 (m)
rho=1000  #densidad agua (kg/m^3)
S=math.pi*D**2/4 

def h_bomba(Q):  #curva de la bomba (dato)        
    return  43-40000*Q**2

def rendimiento(Q):        
    return  180*Q-10000*Q**2

def potencia(Q):
    potencia_fluido = rho*g*h_bomba(Q)*Q
    return  potencia_fluido

def npshr(Q):  #curva de la bomba (dato)        
    return  35-(43-35)+40000*Q**2

Lt=0.014                       #longitud del eje X (rango de caudales en m^3/s)
N = 100                       #numero de puntos a representar
xp = np.linspace(0.0001, Lt, N)    #puntos en x

fig, ax  = plt.subplots(2,2,figsize=(12,8))     #genera el objeto "fig"
ax[0,0].plot(xp,h_bomba(xp))                
ax[0,0].set_title('Curva de altura energética')
#ax[0,0].set_xlabel("$Q(m^3/s)$") 
ax[0,0].set_ylabel("$H(m)$") 


ax[0,1].plot(xp,rendimiento(xp),color="tab:red")                
ax[0,1].set_title('Curva de rendimiento')
#ax[0,1].set_xlabel("$Q(m^3/s)$") 
ax[0,1].set_ylabel('$\eta$') 


ax[1,0].plot(xp,potencia(xp)*0.001,color="tab:green")                
ax[1,0].set_title('Curva de potencia')
ax[1,0].set_xlabel("$Q(m^3/s)$") 
ax[1,0].set_ylabel('$\dot{W}(kW)$') 

ax[1,1].plot(xp,npshr(xp),color="tab:brown")                
ax[1,1].set_title('Curva NPSHR')
ax[1,1].set_xlabel("$Q(m^3/s)$") 
ax[1,1].set_ylabel('NPSHR(m)') 

glue("curvasCaract", fig, display=False)

Las representaciones gráficas anteriores son cualitativas y se han hecho utilizando funciones matemáticas sencillas con las que hemos aproximado las curvas de la bomba. Como se ha indicado anteriormente, las curvas características de una bomba hidráulica se obtienen experimentalmente en un banco de ensayos y son específicas para cada modelo de bomba. Cada bomba tiene su propia curva característica debido a su diseño, tamaño y construcción. Es el fabricante quien debe proporcionar las curvas características de cada modelo de bomba. A continuación se muestra un ejemplo hoja de características de una bomba centrífuga real, en concreto para el modelo Lowara e-SHE 65-160/55/P25VSNA 5,5 KW. 400/690 V.

Fig. 5.9 Hoja de características de una bomba centrifuga Lowara modelo e-SHE 65-160/55/P25VSNA 5,5 KW. 400/690 V. Click aqui para descargar la hoja de características.

5.2.5. Aplicación realista

Para entender mejor estos conceptos, vamos a considerar el siguiente ejemplo.

Ejemplo numérico

Considere una instalación de bombeo de agua entre dos depósitos abiertos a la atmósfera con una diferencia de cota geométrica entre ellos de 36 metros. Los depósitos se conectan a través de una línea compuesta por dos tramos de 5 m (entre el depósito 1 y la bomba) y 500 m (entre la bomba y el depósito 2) respectivamente. Se dispone de un conducto de sección circular (\(D=0.1\) m), para el que asumiremos un factor de fricción constante de \(f=0.02\). Se consideran nulas las pérdidas singulares. Para esta instalación se ha escogido una bomba cuyas curvas características proporcionadas por el fabricante son \(H_{B}(Q)=43-40000Q^2\) y \(\eta(Q)=180Q-10000Q^2\) (unidades en m y m\(^3\)/s).

Fig. 5.10 Instalación del caso de ejemplo.

Para calcular en punto de operación igualaremos la curva de la bomba a la curva de la instalación

\[H_B(Q)=H_I(Q)\]

es decir

\[43-40000Q^2=z_2-z_1 + \frac{fL}{D} \frac{Q^2}{2gS^2}\]

y resolveremos la ecuación.

En Python, definiremos las funciones h_inst(Q) y h_bomba(Q) y resolveremos el punto de operación utilizando la función solve():

##Datos del problema
g=9.81    #aceleración de la gravedad (m/s^2)
f=0.02    #factor de fricción de Darcy
L=5+500   #longitud total conductos (m)
D=0.1     #diámetro conductos (m)
z1=0      #cota depósito 1 (m)
z2=36     #cota depósito 2 (m)
rho=1000  #densidad agua (kg/m^3)

#calculamos la sección de los conductos
S=math.pi*D**2/4 

Q=symbols('Q')

def h_inst(Q):  #curva de la instalación          
    return  z2-z1+f*L/(D*2*g)*(Q/S)**2 

def h_bomba(Q):  #curva de la bomba (dato)        
    return  43-40000*Q**2

#Punto de operación
sol=solve(h_inst(Q)-h_bomba(Q),Q) #para ello utilizamos la función solve(ecuacion,variable), que permite resolver ecuaciones algebraicas
Qp=sol[1]     #la ecuación anterior es cuadrática y tiene 2 soluciones, nos quedamos con la segunda (la positiva)
hp=h_inst(Qp) #evaluamos la curva de la instalación (o de la bomba) en Qp

print("La curva resistente de la instalación es:",h_inst(Q))
print("La curva de la bomba es:",h_bomba(Q))
print("Las soluciones de la ecuación son Q =",sol)
print("El punto de operación es: Qp=",Qp,"m^3/s y hp=",hp,"m")

La curva resistente de la instalación es: 83453.12577269*Q**2 + 36
La curva de la bomba es: 43 - 40000*Q**2
Las soluciones de la ecuación son Q = [-0.00753005199028064, 0.00753005199028064]
El punto de operación es: Qp= 0.00753005199028064 m^3/s y hp= 40.7319326809468 m

Show code cell content Hide code cell content

Lt=0.01                       #longitud del eje X (rango de caudales en m^3/s)
N = 100                       #numero de puntos a representar
xp = np.linspace(0, Lt, N)    #puntos en x
yp1 = h_inst(xp)              #puntos en y: curva instalacion
yp2 = h_bomba(xp)             #puntos en y: curva bomba

fig, ax  = plt.subplots(figsize=(10,7))     #genera el objeto "fig"
ax.plot(xp,yp1,label='Curva resistente de la instalación')        
ax.plot(xp,yp2,label='Curva característica de la bomba')          
ax.plot(Qp,hp,'o') 
ax.plot([0,Qp],[hp,hp],'g--')   
ax.plot([Qp,Qp],[np.min(yp1),hp],'g--')  
ax.set_title('Curvas bomba/instalación')
ax.set_xlabel("$Q(m^3/s)$") 
ax.set_ylabel("$H(m)$") 
ax.legend()
glue("curva_pto", fig, display=False)

Otro cálculo de interés ingenieril es la potencia a suministrar a la bomba (potencia en el eje). Para ello, primero evaluaremos el rendimiento para el caudal obtenido (punto de operación)

\[\eta(Q_p)=180Q-10000Q_p^2\]

y después hallaremos la potencia en el eje utilizando la definición de rendimiento

\[\eta(Q_p)=\frac{\rho g Q_p H_p}{\dot{W}_{eje}}\]

def rendimiento(Q):        
    return  180*Q-10000*Q**2

rto = rendimiento(Qp)
potencia_fluido = rho*g*hp*Qp
potencia_eje = potencia_fluido/rto

print("El rendimiento es:",rto)
print("Potencia fluido:",potencia_fluido, "W")
print("Potencia eje:",potencia_eje," W")

El rendimiento es: 0.788392528487221
Potencia fluido: 3008.86012907850 W
Potencia eje: 3816.44931979752  W

Y llegados a este punto uno uede preguntarse, ¿es esta bomba adecuada para la instalación?. Para saber si hemos elegido bien una bomba, debemos examinar si el punto de operación está cerca del punto de máxima eficiencia (best efficiency point, BEP). Para ello, podemos calcular este punto numéricamente buscando el máximo de la curva de rendimiento:

sol=solve(diff(rendimiento(Q),Q))
Qmax=sol[0]
rtomax=rendimiento(Qmax)

print("El caudal para el cual el rendimiento es máximo es:",float(Qmax), "m^3/s")
print("El rendimiento máximo es:",float(rtomax))

El caudal para el cual el rendimiento es máximo es: 0.009 m^3/s
El rendimiento máximo es: 0.81

Show code cell content Hide code cell content

fig, ax  = plt.subplots(figsize=(10,7)) 

Lt=0.01                          
N = 100                      
xp = np.linspace(0, Lt, N)     
yp1 = h_inst(xp)
yp2 = h_bomba(xp)
yp3 = rendimiento(xp)

ax.plot([Qp, Qp],[35, 44.8],'--',color='tab:gray')
ax.plot([Qmax, Qmax],[35, 45],'--',color='tab:gray')
ax.plot(xp,yp1,label='Curva de la instalación')        
ax.plot(xp,yp2,label='Curva de la bomba')
ax.plot(Qp,hp,'o',label='Punto de operación actual') 
ax.plot(Qmax,h_bomba(Qmax),'*',ms=10,color="tab:green",label='Punto de operación nominal') 


ax2 = ax.twinx()  
color = 'tab:red'
ax2.set_ylabel('$\eta$', color=color)  
ax2.plot(xp,yp3, color=color,label='Rendimiento')
ax2.plot(Qp,rto,'o', color=color)
ax2.plot(Qmax,rtomax,'*',ms=10, color=color)
ax2.tick_params(axis='y', labelcolor=color)

ax.set_title('Curvas bomba/instalación')
ax.set_xlabel("$Q(m^3/s)$") 
ax.set_ylabel("$H(m)$") 
ax.legend(loc='lower right')
ax2.legend()
glue("curva_pto2", fig, display=False)

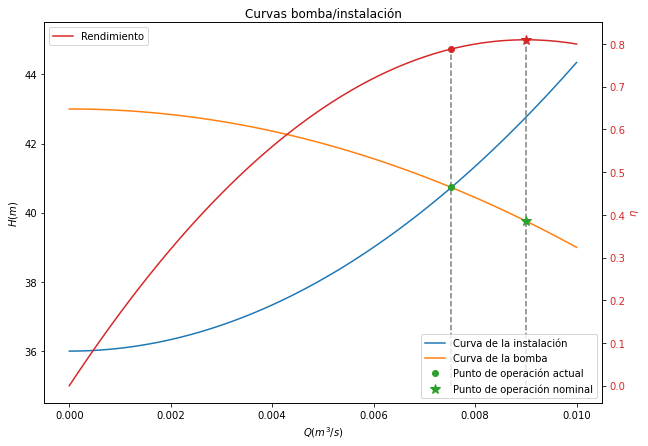
A la vista del resultado obtenido y de la gráfica inferior, se observa que el punto de operación actual está cerca del punto de operación nominal (de máximo rendimiento) y podríamos afirmar que la bomba es adecuada. Estamos trabajando con un rendimiento del 78% y el rendimiento máximo es 81%.

Show code cell content Hide code cell content

k_valvula=0

def h_inst2(Q):
    return  z2-z1+(f*L/D+k_valvula)/(2*g)*(Q/S)**2

#Obtenemos el punto de operación
sol=solve(h_inst2(Q)-h_bomba(Q),Q)
Qp=sol[1]
hp=h_bomba(Qp)

print("La nueva curva de la instalación es:",h_inst2(Q))
print("La curva de la bomba es:",h_bomba(Q))
print("El punto de operación es: Qp=",Qp,"m^3/s y hp=",hp,"m")

LL=0.01
N = 100
xp = np.linspace(0, LL, N)
yp1 = h_inst(xp)
yp2 = h_bomba(xp)
yp3 = h_inst2(xp)

fig, ax  = plt.subplots(figsize=(10,7))
ax.plot(xp,yp1,'tab:blue',label='Sin válvula ($k_v=0$)',lw=3)
ax.plot(xp,yp2,'tab:orange')
ax.plot(Qp,hp,'o')
for i in range(1,14,1):  #hacemos un bucle para pintar varias curvas
    k_valvula=20*i**2
    yp3 = h_inst2(xp)
    ax.plot(xp,yp3,'--',color='tab:blue')
    sol=solve(h_inst2(Q)-h_bomba(Q),Q)
    Qp=sol[1]
    hp=h_bomba(Qp)
    ax.plot(Qp,hp,'o',color='tab:blue')

ax.set_title('Curvas bomba/instalación')
ax.set_xlabel("$Q(m^3/s)$")
ax.set_ylabel("$H(m)$")
ax.annotate("", xy=(0.004, 41), xytext=(0.006, 40),arrowprops={'arrowstyle':'->','lw': 3, 'color': 'tab:green', 'alpha': 1.0})
plt.ylim([min(yp1), max(yp1)])
ax.legend()
glue("curva_pto3", fig, display=False)

La nueva curva de la instalación es: 83453.12577269*Q**2 + 36
La curva de la bomba es: 43 - 40000*Q**2
El punto de operación es: Qp= 0.00753005199028064 m^3/s y hp= 40.7319326809468 m

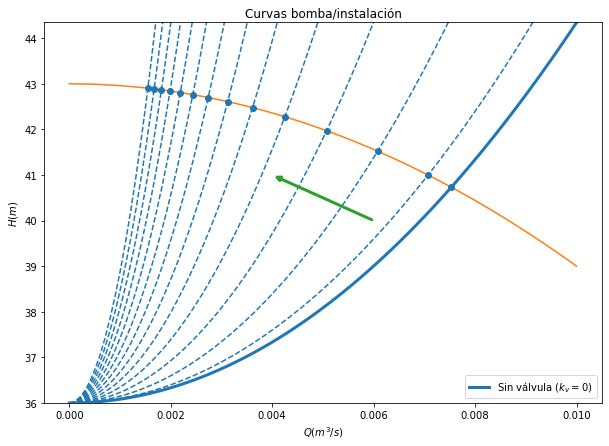
Regulación de caudal

Las instalaciones de fluidos pueden requerir de regulación por diversos motivos: para ajustar el caudal, para ajustar el punto de operación e incrementar la eficiencia, etc. Las estrategias más habituales de regulación de caudal son la regulación por estrangulamiento (cierre de una válvula) a velocidad de giro constante, la regulación por variación de la velocidad de giro de la bomba, y la regulación por variación del ángulo de los álabes en el distribuidor en el rodete. En este ejemplo vamos a considerar la primera de estas estrategias.

Consideremos que colocamos una válvula de estrangulamiento en el tramo de impulsión, cuya constante de pérdidas menores la caracterizamos por \(k_{v}\). ¿Cómo se modificaría el punto de operación al cerrar la válvula?

En este caso la curva resistente de la instalación vendrá dada por:

\[H_I=z_2-z_1+ \left( \frac{fL}{D} +k_{v} \right) \frac{Q^2}{2gS^2}\]

donde observamos que al incrementar el valor de \(k_{v}\), la curvatura de la curva aumenta, desplazando el punto de operación hacia la izquierda, es decir, reduciendo el caudal. Esto se aprecia en la siguiente figura.