1.5. Ley de Newton de la viscosidad

1.5.1. Introducción

Al comienzo de este tema hemos visto que la presencia de esfuerzos cortantes en un fluido producen en éste una deformación angular continua. A continuación se muestra una animación de la deformación continua que experimenta un elemento fluido en el seno de un campo de velocidad con un gradiente en dirección \(y\). Este campo de velocidades e característico de un flujo entre dos placas planas, cuando la placa en el fondo (\(y=0\)) está fija y la placa superior (\(y=5\)) se mueve.

Show code cell content Hide code cell content

import numpy as np              # Librería para poder trabajar con matrices y vectores
import matplotlib.pyplot as plt # Librería para poder dibujar gráficas
from matplotlib import animation
from IPython.display import HTML
from myst_nb import glue

nq=5        #separacion entre vectores en quiver plot
N=50
L=5
xp = np.linspace(0, L, N)
yp = np.linspace(0, L, N)
X, Y = np.meshgrid(xp, yp)

t=0.0
U = Y
V = 0.0*Y

fig, ax = plt.subplots(figsize=(7, 5))
Q = ax.quiver(X[::nq,::nq], Y[::nq,::nq], U[::nq,::nq], V[::nq,::nq])
ax.plot([0,L],[0,0], 'k',lw=6)
ax.plot([0,L],[5,5], 'k',lw=6)
pts = [[1.5,0], [1.5,2], [3.5,2], [3.5,0]]
patch = plt.Polygon(pts, closed=True, alpha=0.5)
ax.add_patch(patch)
pt1, = ax.plot([], [], 'g.', ms=20)
pt2, = ax.plot([], [], 'g.', ms=20)
pt3, = ax.plot([], [], 'g.', ms=20)
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.close()

nframes=50    #frames de la animacion
tf=0.50         #tiempo total
dt=tf/nframes #paso de tiempo

def update_plot(num):
    t = dt*num
    dx=t*2.0
    Q.set_UVC(U[::nq,::nq],V[::nq,::nq])
    patch.set_xy([[1.5,0], [1.5+dx,2], [3.5+dx,2], [3.5,0]])
    pt1.set_data(1.0+t*2.5,2.5)
    pt2.set_data(1.0+t*3.5,3.5)
    pt3.set_data(1.0+t*4.5,4.5)
    return

anim = animation.FuncAnimation(fig, update_plot, frames=nframes, interval=80, blit=False)  

HTML(anim.to_html5_video()) 

1.5.2. Ley de Newton de la viscosidad

Siguiendo con el ejemplo anterior, si analizamos lo que ocurre entre dos capas de fluido, localizadas a una altura \(y\) e \(y+\delta y\), podemos darnos cuenta que éstas se mueven a distinta velocidad:

• Capa en \(y\): La velocidad será \(u\)

• Capa en \(y+\delta y\): La velocidad será \(u+\delta u\)

Debido a la diferencia de velocidad entre ambas capas, existirá un esfuerzo cortante.

Fig. 1.20 Esfuerzos cortantes entre capas de fluido.

Para fluidos newtonianos (luego veremos lo que son), se puede observar experimentalmente que el esfuerzo cortante es proporcional a la velocidad de deformación del elemento diferencial

\[ \tau \propto \frac{\delta \gamma}{\delta t}\]

Fig. 1.21 Deformación en un elemento fluido.

Si consideramos ángulos de deformación \(\delta \gamma\) pequeños

\[ \delta \gamma = \frac{\delta u \delta t}{\delta y}\]

Lo que nos permite expresar

\[ \tau \propto \frac{\delta u}{\delta y}\]

siendo la viscosidad, \(\mu\), la constante de proporcionalidad.

\[ \tau = \mu \frac{\delta u}{\delta y}\]

Tomando el límite para variaciones infinitesimales, obtenemos la ley de Newton de la viscosidad

\[ \boxed{ \tau = \mu \frac{d u}{d y} }\]

Show code cell content Hide code cell content

N = 50
yy = np.linspace(0, L, N) 

def vel(y):
    return (1-((y-L)/L)**2)

uu=vel(yy)

fig, ax = plt.subplots(figsize=(6, 6)) 
ax.plot(uu,yy, color="tab:blue",linewidth=3) 
ax.plot((0,0),(0,L), color="tab:blue", linestyle="--") 
for i in range(0,N,4):   # esto es un bucle para pintar flechas
    ax.annotate("", xy=(uu[i], yy[i]), xytext=(0.0, yy[i]),arrowprops={'arrowstyle':'->','lw': 1.5, 'color': 'tab:blue', 'alpha': 0.7})



yp=2
deltay=1
deltau=2.0/L**2*(yp-L)*deltay
y1=yp-deltay
y2=yp+deltay
up=vel(yp)
u1=up+deltau
u2=up-deltau
ax.plot((u1,u2),(y1,y2), color="k", linestyle="-", lw=3) 
ax.plot((up),(yp), color="k", marker="o") 

ax.plot((up,up+0.2),(yp,yp), color="k", linestyle="--", lw=2)
ax.plot((up+0.2,up+0.2),(yp,yp+0.8), color="k", linestyle="--", lw=2) 

ax.text(0.7, 1.7, 'du', style='italic',fontsize=14)
ax.text(0.87, 2.3, 'dy', style='italic',fontsize=14)

ax.set_xlabel("u(m/s)") # Nombre y unidades del eje x
ax.set_ylabel("y(m)") # Nombre y unidades del eje y
glue("profile_fig", fig, display=False)

A observar…

A la vista de la ley de Newton de la viscosidad

\[ \tau = \mu \frac{d u}{d y}\]

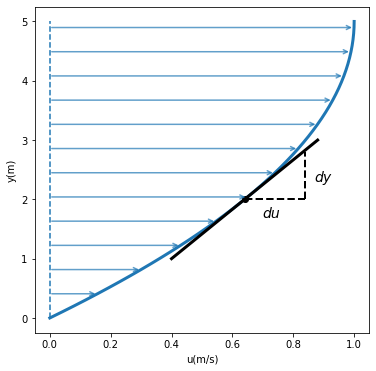
existirá un esfuerzo tangencial siempre que el gradiente de velocidad \(\frac{d u}{d y}\) sea distinto de cero. Este gradiente de velocidad es la pendiente del perfil de velocidades, como se muestra a continuación:

En la figura anterior se muestra un perfil de velocidades parabólico:

\[ u(y)=1-(\frac{y-5}{5})^2\]

Su pendiente es \(-\frac{2}{25}(y-5)\), siendo máxima en \(y=0\) y nula en \(y=5\). Así, el esfuezo cortante será:

• Máximo en \(y=0\).

• Nulo en \(y=5\).